ความต้านทานในการเคลื่อนที่ของวัตถุนั้นเราจะเรียกว่าความเฉื่อยของวัตถุ ในกรณีที่วัตถุนั้นเคลื่อนที่เป็นแนวเส้นตรงความเฉื่อยของวัตถุนั่นก็คือมวลของวัตถุนั่นเอง และในกรณีที่วัตถุเคลื่อนที่แบบหมุน ความเฉื่อยของวัตถุที่ต้านทานการหมุนนั้นเราเรียกว่า โมเมนต์ความเฉื่อย ซึ่งการที่จะทำให้วัตถุเคบื่อนที่แบบหมุนได้ด้วยความเร็วเชิงมุมที่ต้องการนั้น เราจำเป็นต้องใส่แรงบิดเข้าไป โดยที่แรงบิดนี้จะแปรผันโดยตรงกับโมเมนต์ความเฉื่อยของวัตถุนั้น ซึ่งสมการของแรงบิดกับโมเมนต์ความเฉื่อยนั้นสามารถหาได้ดังนี้
T=Iα
T คือ แรงบิดที่ใส่เข้าไปให้ในวัถุเพื่อให้เกิดการหมุน
I คือ โมเมนต์ความเฉื่อยของวัตถุตามแนวแกนหมุน
α คือ ความเร่งเชิงมุมของการหมุนของวัตถุ
ในระบบวัตถุอย่างง่ายอย่างเช่นวัตถุมวล m หมุมรอบแกนหมุนหนึ่งโดยที่วัตถุนี้อยู่ห่างจากแกนหมุนเท่ากับ r แล้วจะสามารถคำนวนโมเมนต์ความเฉื่อยได้ดังสมการ
I = mr²
แต่งานในชีวิตประจำวันมันไม่ง่ายเลยที่จะคำนวนโมเมนต์ความเฉื่อยด้วยมือ ความซับซ้อนของเครื่องจักรทำให้เกิดความซับซ้อนในการคำนวนหาโมเมนต์ความเฉื่อยของชิ้นงาน แต่มันกลับทำได้ง่ายมากเพียงการใช้คำสั่ง Mass Properties

และนี่คือตัวอย่างผลของโมเมนต์ความเฉื่อยที่คำนวนได้
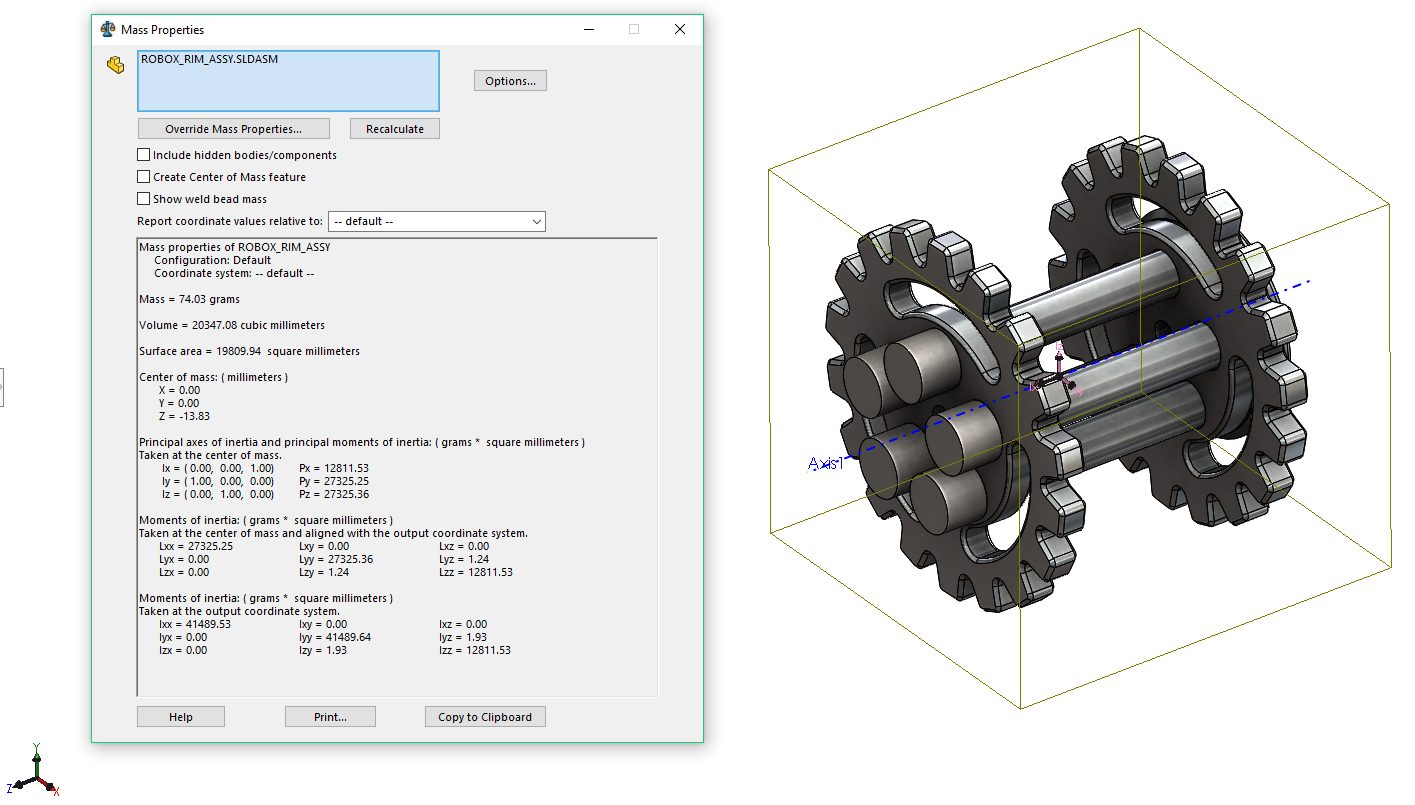
ผลที่ได้จากการคำนวนนั้นมีโมเมนต์ความเฉื่อยแสดงออกมาด้วยกัน 3 รูปแบบ คือ
- Principal axes of inertia and Principal moment of inertia taken at the center of mass
- Moment of inertia taken at the center of mass and align with the output coordinate
- Moment of inertia taken at output coordinate
ซึ่งคำถามที่ตามมานั่นคือแล้วเราจะใช้ โมเมนต์ความเฉื่อยค่าไหนในการคำนวนแรงบิดเพื่อที่จะให้ชิ้นงานหมุนในทิศทางแกน Axis1 ในความเร็วที่เราต้องการ
ก่อนที่เราจะรู้ว่าควรใช้ค่าโมเมนต์ความเฉื่อยค่าไหน เรามาทำความรู้จักโมเมนต์ความเฉื่อยในแต่ละชนิดที่ SOLIDWORKS แสดงออกมา
Principal axes of inertia and Principal moment of inertia taken at the center of mass เป็นโมเมนต์ความเฉื่อยที่คิดที่ตำแหน่งจุดศูนย์กลางมวลของวัตถุ โดยที่แกนโมเมนต์ความเฉื่อยที่คำนวนนี้จะเป็นแกน Principal นั้นคือ ชิ้นงานที่หมุนรอบแกนใดๆของ แกน Principal แล้วจะมีการหมุนแบบเสถียรและไม่มีการสั่นเกิดขึ้นในการหมุน ทิศทางแกน Principal นั้นจะแสดงเป็นแกนสีชมพูติดอยู่ที่จุดศูนย์กลางมวลของชิ้นงาน
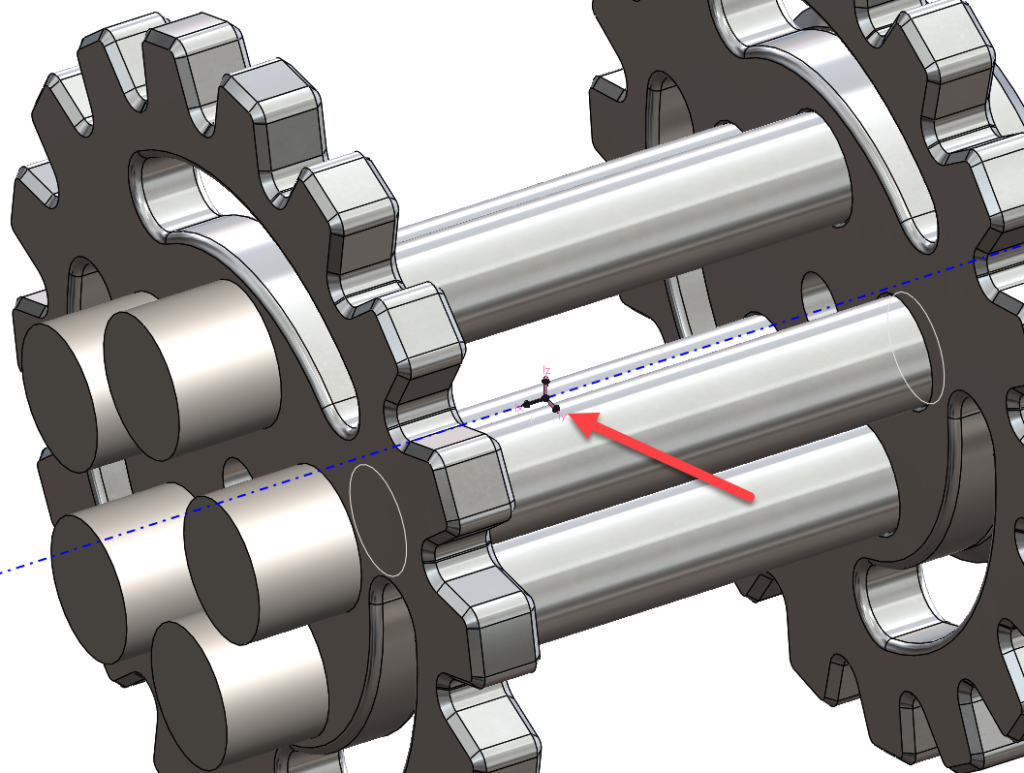
และในกรณีจะเห็นว่าแกน IX ของ Principal นั้นมีแนวเดียวกันกับ แกน Axis1 ที่ต้องการให้ชิ้นงานหมุนดังนั้นค่าโมเมนต์ความเฉื่อยที่ใช้ในการคำนวนแรงบิดนั้นมีค่าเท่า Px = 12811.53 และการหมุนของชิ้นงานรอบแกน IY หรือ IZ ณ ตำแหน่งการหมุนที่จุดศูนย์กลางมวลนี้นั้นชิ้นงานจะหมุนได้อย่างเสถียร และไม่เกิดการสั่น
Moment of inertia taken at the center of mass and align with the output coordinate โมเมนต์ความเฉื่อยแบบนี้คิดที่ตำแหน่งจุดศูนย์กลางมวล แต่ทิศทางแกนของโมเมนต์ความเฉื่อยนั้นเป็นทิศทางเดียวกันกับ Default Coordinate หรือ จุดออริจินนั่นเอง และจะเห็นว่าแกน Axis1 นั้นมีการวางตัวไปในทางแกน Z ของ Default Coordinate ดังนั้นค่าโมเมนต์ความเฉื่อยที่ต้องการนำไปใช้ในการคำนวนแรงบิดนั้นจึงต้องใช้ค่า IZZ = 12811.53 และการหมุนของชิ้นงานรอบแกน Y หรือ Z ณ ตำแหน่งการหมุนที่จุดศูนย์กลางมวลนี้นั้นชิ้นงานจะหมุนได้อย่างเสถียร และไม่เกิดการสั่น
Moment of inertia taken at output coordinate โมเมนต์ความเฉื่อยแบบนี้จะคิดที่ตำแหน่งจุด Output Coordinate ซึ่งก็คือ Default Coordinate หรือจุดออริจินนั่นเอง (ถ้าไม่กำหนด Output Coordinate ให้เป็นจุดอื่น) ดังนั้นค่าโมเมนต์ความเฉื่อยที่ต้องการนำไปใช้ในการคำนวนแรงบิดนั้นจึงต้องใช้ค่า IZZ = 12811.53 และการหมุนของชิ้นงานรอบแกน Y หรือ Z ณ ตำแหน่งการหมุนที่จุดศูนย์กลางมวลนี้นั้นชิ้นงานจะหมุนได้อย่างเสถียร และไม่เกิดการสั่น และเมื่อพิจารณค่าโมเมนต์ความเฉื่อยของแกน Y และ Z เมื่อเทียบกับโมเมนต์ความเฉื่อยแบบอื่นแล้วพบว่าค่าโมเมนต์ความเฉื่อยนั้นมีค่ามากว่าเกือบสองเท่านั้นแปลว่าในการจะหมุนชิ้นงานนี้รอบจุดออริจินในทิศทางแกน Y หรือ Z นั้นจะต้องใช้แรงบิดมากว่าเกือบสองเท่าเมื่อเทียบการการหมุนชิ้นงานรอบจุดศูนย์กลางมวล
ดังนั้นในการเลือกใช้โมเมนต์ความเฉื่อยนั้นสามารถเลือกใช้รูปแบบไหนก็ได้แต่ต้องตรวจสอบแกนของการหมุนว่าไปตรงกับแกนไหนของดมเมนต์ความเฉื่อยชนิดนั้นๆ

ความเข้าใจในเรื่องของโมเมนต์ความเฉื่อยประกอบกับความง่ายในการคำนวนหาโมเมนต์ความเฉื่อยของ SOLIDWORKS นี้ ช่วยให้วิศวกรสามารถคำนวนแรงบิดที่ต้องการได้อย่างถูกต้องและสามารถที่กำหนดตำแหน่งจุดหมุนของชิ้นงานที่สมดุลและเสถียรซึ่งจะช่วยลดภาระกรรมที่อาจเกิดบนชิ้นงานรองเพลาหมุนอย่างเช่นแบริ่งได้ และนั่นคือเป็นการลดต้นทุนของการผลิตได้อย่างดี
บทความโดย แอดโจ๊ก
